At Last....DECIMALS!!!

The time is here were we come to the last post of this blog.  This last post I wanted to focus on a topic that can be difficult to a lot of students. The DECIMAL!!! Some children and adults find the period very intimidating because when multiplying decimals together you are not only trying to figure out the correct numericals, but you also have to know if you can leave the decimal in its place or move the decimal to a different position of the number.





With the example, as a student I would atutomiatically get confused because you have some problems with decimals being multiplied by whole numbers and by other deceimal numbers, but the decimals are lined up together.  So first we have to go over the stepts to multiplying with decimals.

Steps to Multyiplying Decimals:

1. Multiply like whole numbers.

2. Count decimal places in the problem.

3. Put the same number of places beind the decimal in the product.

Here below is an example of how two decimals would be multiplied together.




From the very first problems that was given above the student would have to multiply

a. 4.6                b. 3.9                 c. 14.56
   x  7                  x5.6                    x   2.8

  32.2                   234                    11648
                          1950                    29120
                         21.84                   40.768

Another way to try to figure out where the decimal point goes and that is by rounding the two multiplying numbers to the nearest whole number. After solving the product of those two numbers that is where you will place your decimal point. I found this way by watcing this video that is provided below.

Perform operations with multi-digit whole numbers and with decimals to hundredths.

CCSS.MATH.CONTENT.5.NBT.B.7
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.

Did I Divide That?!?!?

Fractions can come easy or hard to some people when doing it in math class.  For me is was quite simple, but once my teachers tried to teach me that two fractions can be divided by each other I becae the biggest confused person in the classroom.  I needed extra help and once I got the help I had to teach myself that there is one important step that has to be taken before I can complete the problem.  I would always forget to flip the fraction before soloving.  This week I wanted to focus on dividing fractions.

When I was a student and I had saw a similar problem like this I was very confused on what was done and why it was done that way.  Below are some steps to solving a fraction divided by another fraction.

Steps:

1. The problem is given as a division problem.  It must be rewritten to a multiplication problem by simply reversing the fraction recipricol to the divisor.

2. Then you multiply the numerator and the denominator.

3. Then simplify if necessary.

So using the first example given the student(s) would have to solve the problem like this:


1  ➗  1  ͇     1 ✖  4   ͇    4   ͇͇   2
2         4       2       1      2



CCSS.MATH.CONTENT.5.NF.B.7
Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.

Apply and extend previous understandings of multiplication and division to divide fractions by fractions.

CCSS.MATH.CONTENT.6.NS.A.1
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?.

Fractions X's Whole Numbers

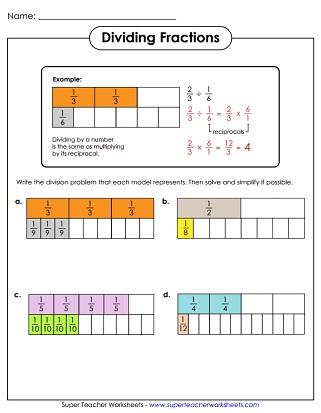
When I was learning about multiplying fractions one conept that used to confuse me was multiplying a fraction by a whole number.  This past class reminded me of that when we the professor gave us an identical example problem.  If I was presented with the problem 3/4 x 7. I knew that I would have to change the 7 into a fraction so I would put 7/7.  The problem with that 7/7 is equaled to 1. So this week I will be focusing on the steps to multiplying a fraction by a whole number.

Above is an example of whole number multiplied by a fraction. Here are the steps that I and students can use in order to solve the problem.

Steps:

1. Rewrite the whole number as a fraction. To rewrite a whole number as a fraction, simply place the whole number over 1. (Any number over one is equaled to itself.)

2. Multiply the numerators of the two fractions. (The numerators are the numbers above the line.)

3. Multiply the denominators of the two fractions. (The denominators are the numbers below the line.)

4. Reduce the answer if possible.  Your answer most likley will become a proper fraction or an imporper fraction, you have to simplify the answer to its lowest terms.  The number in the denominator will have to be divided by the numerator and the denominator to equal your simplified answer.

By using the steps above for the example 3 x 2/15 the answer would be:

 3    x   2   =  6     =    2 

 1        15      15         5

Here is another example of a whole number multiplied by a fraction that is turned into an improper fraction and simplified:

 

Multiplying whole numbers by fractons can also be shown in models because multiplication is nothing more than repeated addition. So below is a model to show how it multiplyng whole numbers by fractions can be used a a different way:

Though some students might not be comfortable with word problems, they should be able to understand and extract the key details that is needed to solve a word problem.  I would provide the students with a fun word problem activity for them to do individually or in pairs.

CCSS.MATH.CONTENT.4.NF.B.4
Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.

CCSS.MATH.CONTENT.4.NF.B.4.A
Understand a fraction a/b as a multiple of 1/b. For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).

CCSS.MATH.CONTENT.4.NF.B.4.B
Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)

CCSS.MATH.CONTENT.4.NF.B.4.C
Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?

STOP.....IT'S FRACTION TIME!!!!

So far we have covered multiplying single & double digit numbers, long multiplication, and multiplication including addition.  This week I will be covering mulitplying fractions.  Fractions may can be simple for students when trying to identify a portion of a large quanity. A circle that is divided in half and shaded is equalled to 1/2 and a square that is cut into 4 squares and three of them are shaded is equalled to 3/4. Though that can be easy, some students might find it difficult when they want to find out how much of the shaded areas combined equals up too. Here is a video below to show students how to multiply fractions.

After the students become familarized with the song the students should be presented with the three step process of multiplying fractions.

Steps for Multiplying Fractions:

1. Multiply the numerator.

2. Multiply the denomicator.

3. Reduce the fraction if necessary.





After we revisit the parts of a fraction from the example of above I would then give students an example of how to multiple a fraction by used the three step process.




Below is a work sheet that can be given to students for them to practice on.



For an even fun activity you can group students in to pairs and have them give each other there own fraction multiplication problems by providing them with a blank sheet.

CCSS.MATH.CONTENT.5.NF.B.4
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction

CCSS.MATH.CONTENT.5.NF.B.4.A
Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = (ac)/(bd).

Step by Step...Plus!

During my posts I have only been focusing on how solve math problems or word problems by using multiplication. Students are going to learn that not all problems are multiplication problems.  Some multiplication problems and word problems include addition.  With the problems you are going to have to use MULTIPLE STEPS.

Steps to solving a Multiplication & Additon Problem:

Step 1: Look at the problem
Step 2: Identify the two multiplying numbers
Step 3: Retrieve the product from the two numbers
Step 4: Add the product and the other number to solve the problem.



By using the multiplication steps a student would be able to answer the problem as:

1. 7 x 4 + 2=               2. 3 x 7 + 8=           3. 6 x 4 + 2=
     
    28 + 2= 30                  21 + 8= 29               24 + 2= 30


When students are given a multistep word problems these same rules must be applied, but they are given more of a challenge because they must read the problem first.


Steps to solving a Multiplication & Additon Word Problem:

Step 1: Read the problem
Step 2: Identify the key words/numbers
Step 3: Identify the multiplying numbers
Step 4: Retrieve the product from the two numbers
Step 5: Add the product and the other number to solve the problem.




To solve problem #3 students would highlight important clues:

- Polly 22 marbles
- 5 bags of marbles
- 8 marbles in each bag

Once identifying that the two multiplying numbers are 5 & 8 the studet will multiply them:

5 x 8=40 marbles

Lastly the student will have to add the product (40 marbles) by 22 marbles:

40 + 22= 62 marbles


Common Core Standards:

CSS.MATH.CONTENT.5.OA.A.
Write simple expressions that record calculations with numbers, and interpret numerical expressions without evaluating them. For example, express the calculation "add 8 and 7, then multiply by 2" as 2 × (8 + 7). Recognize that 3 × (18932 + 921) is three times as large as 18932 + 921, without having to calculate the indicated sum or product.

CCSS.MATH.CONTENT.4.OA.A.3
Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

What's That Method?

When introducting long multiplication into the curriculumn, educators know that there will be some fairness, hesitation, and difficulty when present to students.  There are some students who will find it easy and grasp the material easily.  Then there will be some students who truly find it difficult to do and they may become frustrated and flustered.  When I was in school multiplication was introduced one type of way, with a number on the type, a multiplying number on the bottom and a line underneath it.  Until this day I still multiply my numbers the same way, but times have changed and math as evolved so there are an abundant amount of methods that can be used for long multiplication.

Once the students have watched the video they can be given more than one method ot find the product of there multiplication problem.

The first method of finding the answer to long multiplication is a COLUMN METHOD.

 A second method that can be demonstrated for students is the Lattice Method.

By providing students with different methods to solve a long multiplication problem we are offering students different choices to choose from to retrieve the correct and same answer.

CCSS.MATH.CONTENT.4.NBT.B.5
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.

What's The WORD!!!

Solving word problems could be difficult for some people because they have to do multiple steps when trying to figure out the answer.  

Step 1: Read the problem 

Step 2: Identify the key words/numbers

Step 3: Set up the mathematical problem

Step 4: Solve the problem

Below is a video which can help students and adults help understand better how to solve multiplication problems.

After completing the video possibly once or twice you should try to apply what you learned in the video to word problems. 

CCSS.MATH.CONTENT.3.OA.A.3
Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.

CCSS.MATH.CONTENT.3.OA.C.7
Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers